GCSE EDEXCEL Calculations Involving Masses

Limitations of Models

Specification Point 1.41:

• Describe the limitations of particular representations and models, to include dot and cross, ball and stick models and two- and three-dimensional representations.

• There are different ways of representing atoms and molecules depending on the type of substance in question.
• Each method has its advantages and disadvantages.
• The main limitation is that although it is relatively easy to represent smaller molecules, larger and more complex molecules are difficult to show graphically.

Dot and Cross Diagrams

• Advantages:
  • Useful for illustrating covalent compounds as they can show the sharing of electrons.
  • Indicate from which atom the bonding electrons come from.
• Disadvantages:
• Fail to illustrate the 3D arrangements of the atoms and electron shells.
• Cannot indicate the relative sizes of the atoms.

Dot and Cross model of ammonia showing how the electrons are shared between the N and H atoms

Ball and Stick Model

• Advantages:
  • Useful for illustrating the arrangement of atoms in 3D space.
  • Very useful for visualizing the shape of a molecule.
• Disadvantages:
• Fail at indicating the sharing or movement of electrons.
• The atoms are placed far apart from each other, which in reality is not the case as the gaps between atoms are much smaller.

Ball and stick model of ammonia which illustrates the 3D arrangement of the atoms in space and the shape of the molecule

2D Representations of Molecules

• Advantages:
  • Displayed formulae are 2D representations and are basically simpler versions of the ball and stick model.
  • Adequately indicate what atoms are in a molecule and how they are connected.
• Disadvantages:
• Fail to illustrate the relative sizes of the atoms and bonds.
• Cannot give you an idea of the shape of a molecule and what it looks like in 3D space.

Displayed formula of ammonia

3D Representations of Ionic Solids

• Advantages:
  • 3D drawings and models depict the arrangement in space of the ions.
  • Also show the repeating pattern in giant lattice structures.
• Disadvantages:
• Only illustrate the outermost layer of the compound.
• Are difficult and time-consuming to draw.

3D representation of the ionic lattice structure of silver fluoride. The silver atoms are in blue/grey and the fluorine atoms in green

Relative Atomic Mass

Specification Point 1.43:

• Calculate relative formula mass given relative atomic masses.

• The symbol for the relative formula mass is Mr and it refers to the total mass of the molecule.
• To calculate the Mr of a substance, you have to add up the relative atomic masses of all the atoms present in the formula.
• The relative atomic masses of every element is available on The Periodic Table, it is the larger of the two numbers. 

Examples:

Formulae of Simple Compounds

Specification Point 1.44:

• Calculate the formulae of simple compounds from reacting masses and understand that these are empirical formulae.

• The empirical formula gives the simplest whole number ratio of atoms of each element in the compound.
• It is calculated from knowledge of the ratio of masses of each element present.
• Use the equation for calculating the number of moles from mass:
  • Moles = mass ÷ M_r
• The mole is a unit of measurement used in chemistry.
• The relative atomic mass of an element is exactly equal to the mass of one mole of that element.
• The same applies for a compound.
• For example the relative molecular mass of carbon dioxide is: 12 + (16 x 2) = 44.
• So one mole of CO₂ has a mass of 44g.

Example 1:

Show that a compound which contains 10g of hydrogen and 80g of oxygen has an empirical formula of H₂O.

Amount of hydrogen atoms = mass in grams ÷ A_r of hydrogen = (10 ÷ 1) = 10 moles

Amount of oxygen atoms = mass in grams ÷ A_r of oxygen = (80 ÷ 16) = 5 moles

The ratio of moles of hydrogen atoms to moles of oxygen atoms:

                      Hydrogen            Oxygen

Moles                 10             :            5

Ratio                   2              :            1

Since equal numbers of moles of atoms contain the same number of atoms, the ratio of hydrogen atoms to oxygen atoms is 2:1

Hence the empirical formula is H₂O

Example 2:

What is the empirical formula of a compound that contains 7.83g of iron and 3.37g of oxygen?

Amount of iron atoms = mass in grams ÷ A_r of iron = (7.83 ÷ 55.85) = 0.14 moles

Amount of oxygen atoms = mass in grams ÷ A_r of oxygen = (3.37 ÷ 16) = 0.21 moles

The ratio of moles of iron atoms to moles of oxygen atoms:

                           Iron                  Oxygen

Moles                 0.14             :            0.21

Divide across by the smallest number (0.14):

Ratio                   1                 :            1.5

Simplify to the nearest whole number (multiply across by 2):

Ratio                   2                 :            3

Hence the empirical formula is Fe₂O₃

Empirical and Molecular Formulae

Specification Point 1.45:

• Deduce:
  a) the empirical formula of a compound from the formula of its
  Molecule
  b) the molecular formula of a compound from its empirical formula and its relative molecular mass

• The empirical formula tells you the simplest whole number ratio of atoms in a compound.
• The molecular formula tells you the actual number of atoms of each element in one molecule of the compound or element e.g. H₂ has 2 hydrogen atoms, HCl has 1 hydrogen atom and 1 chlorine atom.

Deducing empirical formula

• The empirical formula can be deduced from the molecular formula.
• Do this by simplifying the number of each atom by dividing across by the largest whole number that will divide evenly into each number in the molecular formula.

Examples:

Deducing molecular formula

• Divide the relative formula mass of the molecular formula by the relative formula mass of the empirical formula.
• Then multiply the number of each element present in the empirical formula by this number to find the molecular formula.

Example:

The Empirical Formula of X is C₄H₁₀S₁ and the Relative Formula Mass of X is 180. What is the Molecular Formula of X?

Relative Formula Mass:       Carbon : 12      Hydrogen : 1      Sulfur : 32

Step 1 Calculate Relative Formula Mass of Empirical Formula

(C x 4) + (H x 10) + (S x 1)    =   (12 x 4) + (1 x 10) + (32 x 1)   =   90

Step 2 Divide Relative Formula Mass of X by Relative Formula Mass of Empirical

Formula

               180 / 90 = 2

Step 3 Multiply Each Number of Elements by 2

(C_{4 x 2}) + (H_{10 x 2}) + (S_{1 x 2})     =    (C₈) + (H₂₀) + (S₂)

                                                                              Molecular Formula of X = C₈H₂₀S₂

Plan an Investigation to Determine Empirical Formula

Specification Point 1.46:

• Describe an experiment to determine the empirical formula of a simple compound such as magnesium oxide.

• There are two methods to carry out this investigation:
  • Method A: Combustion of magnesium oxide
  • Method B: Reduction of magnesium oxide

Method A: Combustion of Magnesium Oxide

Diagram of the apparatus to find the formulae of a metal oxide by combustion

Method:

• Measure and record the mass of crucible and lid
• Add sample of metal into crucible and measure mass with lid and record
• Strongly heat the crucible over a Bunsen burner for several minutes
• Frequently lift the lid to allow sufficient air into the crucible for the metal to fully oxidise but without letting any of the gaseous metal oxide to escape
• Continue heating until the mass of crucible remains constant 
• Measure the mass of crucible and contents and record

Calculation of empirical formula:

• Mass of metal = (mass of crucible + lid + metal) – (mass of crucible + lid)
• Mass of metal oxide = (mass of crucible + lid + oxide) – (mass of crucible + lid)
• Mass of oxygen = mass of metal oxide – mass of metal
• Step 1 Divide each of the two masses by their Relative Atomic Masses
• Step 2 Simplify the ratio

Metal            Oxygen

Mass               x                       y

Mole              x / M_r               y / M_r

     = a                   = b

Ratio                a          :           b

• Step 3 Write out the formula using the ratio e.g. for magnesium: Mg_aO_b

Method B: Reduction of Magnesium Oxide

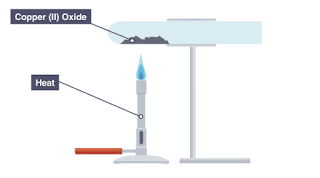
Diagram of the apparatus to find the formulae of a metal oxide by reduction

Method:

• Measure and record the mass of the metal oxide
• Use a clamp to hold boiling tube horizontally, and place the metal oxide at the end of the tube
• Heat using a Bunsen burner until all  the oxide has completely changed colour, indicating that all the oxygen has been reduced
• Measure and record the mass of the remaining powder

Calculation of empirical formula:

• Mass of metal = mass of remaining metal powder
• Mass of oxygen = (mass of metal oxide) – (mass of metal powder)
• Step 1 Divide each of the two masses by their Relative Atomic Masses
• Step 2 Simplify the ratio

Metal            Oxygen

Mass               x                       y

Mole              x / M_r               y / M_r

    = a                   = b

Ratio                a          :           b

• Step 3 Write out the formula using the ratio e.g. for copper: Cu_aO_b