IGCSE CHEMISTRY 0620 Cambridge LESSON 8 EXPLANATION

Lesson  8

4.2 The mole concept

• Define the mole and the Avogadro constant

The mole

• This is the mass of substance containing the same number of fundamental units as there are atoms in exactly 12.000 g of ¹²C.
• The mole is the unit representing the amount of atoms, ions, or molecules.
• One mole is the amount of a substance that contains 6.02 x 10²³ particles (Atoms, Molecules or Formulae) of a substance (6.02 x 10²³ is known as the Avogadro Number).

Examples

• 1 mole of Sodium (Na) contains  6.02 x 10²³  Atoms of Sodium
• 1 mole of Hydrogen (H₂) contains  6.02 x 10²³  Molecules of Hydrogen
• 1 mole of Sodium Chloride (NaCl) contains  6.02 x 10²³  Formula units of Sodium Chloride

Linking the mole and the atomic mass

• One mole of any element is equal to the relative atomic mass of that element in grams.
• For example one mole of carbon, that is if you had 6.02 x 10²³ atoms of carbon in your hand, it would have a mass of 12g.
• So one mole of helium atoms would have a mass of 4g, lithium 7g etc.
• For a compound we add up the relative atomic masses.
• So one mole of water would have a mass of 2 x 1 + 16 = 18g.
• Hydrogen which has an atomic mass of 1 is therefore equal to 1/12 mass of a ¹²C atom.
• So one carbon atom has the same mass as 12 hydrogen atoms.

• Use the molar gas volume, taken as 24 dm3 at room temperature and pressure

Molar volume

• This is the volume that one mole of any gas (be it molecular such as CO₂ or monoatomic such as helium) will occupy.
• Its value is 24dm³ or 24,000 cm³ at room temperature and pressure (r.t.p.)

Calculations Involving Gases
General Equation:

 

1. Calculating the volume of gas that a particular amount of moles occupies.
Equation:
                        Volume of Gas (dm³)      =      Amount of Gas  (mol)     x    24    
                        or             
                        Volume of Gas (cm³)      =     Amount of Gas (mol)     x    24000
Example:

 

2.  Calculating the moles in a particular volume of gas.
Equation:

Example:

• Calculate stoichiometric reacting masses, volumes of gases and solutions, and concentrations of solutions expressed in g / dm3and mol / dm3. (Calculations involving the idea of limiting reactants may be set. Questions on the gas laws and the conversion of gaseous volumes to different temperatures and pressures will not be set.)

Calculating percentage composition, moles, mass and relative formula mass

Formula triangle for moles, mass and formula mass

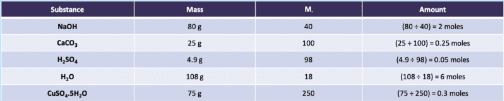
1. Calculating moles
Equation:

 

Example:

 

2. Calculating mass
Equation:

Example:

 

3. Calculating relative formula mass:
Equation:

Example:
10 moles of Carbon Dioxide has a Mass of 440 g. What is the Relative Formula Mass of Carbon Dioxide?
Relative Formula Mass = Mass ÷ Number of Moles
Relative Formula Mass = 440 ÷ 10 = 44
                                                     Relative Formula Mass of Carbon Dioxide = 44
4. Calculating Percentage Composition

• The percentage composition is found by calculating the percentage by mass of each particular element in a compound.

Example:
Calculate the percentage of oxygen in CO₂.
Step 1 – Calculate the molar mass of the compound
               Molar mass CO₂  =  (2 x 16) + 12   =  44
Step 2 – Add the atomic masses of the element required as in the question (oxygen)
               16 + 16 = 32
Step 3 – Calculate the percentage
   % of oxygen in CO₂ = 32/44 x 100 = 72.7%
Calculations of solutions: moles, concentration and volume
General Equation:

This general equation is rearranged for the term as is asked in the question.

• Calculating Moles

Equation:

Example:
Calculate the Moles of Solute Dissolved in 2 dm³ of a 0.1 mol / dm³ Solution
Concentration of Solution : 0.1 mol / dm³
Volume of Solution : 2 dm³
Moles of Solute   =   0.1   x   2   =   0.1 mol (the dm³ above and below the line cancel out)
                                                                                         Amount of Solute = 0.2 mol

2.  Calculating Concentration

Equation:

Example:
25.0 cm³ of 0.050 mol / dm³ sodium carbonate was completely neutralised by 20.00 cm³ of dilute hydrochloric acid. Calculate the concentration, in mol / dm³ of the hydrochloric acid.
Step 1 – Calculate the amount, in moles, of sodium carbonate reacted by  rearranging the equation for amount of substance (mol) and dividing by 1000 to convert cm³ to dm³
Amount of Na₂CO₃  =  (25.0 x 0.050) ÷ 1000  =  0.00125 mol
Step 2 – Calculate the amount, in moles, of hydrochloric acid reacted
Na₂CO₃  +  2HCl  →  2NaCl  +  H₂O  +  CO₂
1 mol of Na₂CO₃ reacts with 2 mol of HCl, so the Molar Ratio is 1 : 2
Therefore 0.00125 moles of Na₂CO₃ react with 0.00250 moles of HCl
Step 3 – Calculate the concentration, in mol / dm³ of the Hydrochloric Acid
1 dm³ = 1000 cm³
Volume of HCl =  20 ÷ 1000  =   0.0200 dm³
Concentration HCl (mol / dm³) =  0.00250 ÷ 0.0200  =  0.125
                                         Concentration of Hydrochloric Acid = 0.125 mol / dm³

3. Calculating Volume
Equation:

Example:
Calculate the volume of hydrochloric acid of concentration 1.0 mol / dm³ that is required to react completely with 2.5g of calcium carbonate.
Step 1 – Calculate the amount, in moles, of calcium carbonate that reacts
M_r of CaCO₃ is 100
Amount of CaCO₃  =  (2.5 ÷ 100)  =  0.025 mol
Step 2 – Calculate the moles of hydrochloric acid required
CaCO₃  +  2HCl  →  CaCl₂  +  H₂O  +  CO₂
1 mol of CaCO₃ requires 2 mol of HCl
So 0.025 mol of CaCO₃ Requires 0.05 mol of HCl
Step 3 – Calculate the volume of HCl Required
Volume  =  (Amount of Substance(mol)  ÷  Concentration (mol / dm³)
=  0.05  ÷  1.0
=  0.05 dm³ (the moles cancel out above and below the line)
                                                                 Volume of Hydrochloric Acid = 0.05 dm³

The limiting reactant and reacting masses
Limiting reactant

• The limiting reactant is the reactant which is not present in excess in a reaction.
• It is always the first reactant to be used up which then causes the reaction to stop.
• In order to determine which reactant is the limiting reagent in a reaction, we have to consider the ratios of each reactant in the balanced equation.

Example:
9.2g of sodium is reacted with 8.0g of sulfur to produce sodium sulfide, NaS. Which reactant is in excess and which is the limiting reactant?
Step 1 – Calculate the moles of each reactant
Moles = Mass ÷ A_r
Moles Na = 9.2/23 = 0.40
Moles S = 8.0/32 = 0.25
Step 2 – Write the balanced equation and determine the molar ratio
2Na + S → Na₂S so the molar ratios is 2 : 1
Step 3 – Compare the moles. So to react completely 0.40 moles of Na require 0.20 moles of S and since there are 0.25 moles of S, then S is in excess. Na is therefore the limiting reactant.

Calculating reacting masses

• Chemical equations can be used to calculate the moles or masses of reactants and products.
• Use information from the question to find the amount in moles of the substances being considered.
• Identify the ratio between the substances using the balanced chemical equation.
• Apply mole calculations to find answer.

Example 1:
Calculate the Mass of Magnesium Oxide that can be made by completely burning 6 g of Magnesium in Oxygen
Magnesium (s)  + Oxygen (g)  →   Magnesium Oxide (s)
Symbol Equation:     2Mg     +     O₂       →       2MgO
Relative Formula Mass:    Magnesium : 24             Magnesium Oxide : 40
Step 1 – Calculate the moles of Magnesium Used in reaction
Moles = Mass ÷ M_r                                       Moles = 6 ÷ 24 = 0.25
Step 2 – Find the Ratio of Magnesium to Magnesium Oxide using the balanced Chemical Equation

Step 3 – Find the Mass of Magnesium Oxide
Moles of Magnesium Oxide = 0.25
Mass = Moles x M_r                                       Mass = 0.25 x 40 = 10 g
                                                            Mass of Magnesium Oxide Produced = 10 g

Example 2:
Calculate the Mass, in Tonnes, of Aluminium that can be Produced from 51 Tonnes of Aluminium Oxide
Aluminium Oxide (s)  →   Aluminium (s)   +   Oxygen (g)
Symbol Equation:     2Al₂O₃     →       4Al       +       3O₂
A_r and M_r:                   Aluminium : 27    Oxygen : 16    Aluminium Oxide : 102
1 Tonne = 10⁶ g
Step 1 – Calculate the moles of Aluminium Oxide Used
Mass of Aluminium Oxide in Grams = 51 x 10⁶ = 51,000,000  g
Moles = Mass ÷ A_r                             Moles = 51,000,000 ÷ 102 = 500,000
Step 2 – Find the Ratio of Aluminium Oxide to Aluminium using the balanced Chemical Equation

Step 3 – Find the Mass of Aluminium
Moles of Aluminium = 1,000,000
Mass in grams = Moles x A_r                Mass = 1,000,000 x 27 = 27,000,000
Mass in Tonnes = 27,000,000 ÷ 10⁶ = 27 Tonnes
                                                               Mass of Aluminium Produced = 27 Tonnes

Empirical Formula: Gives the simplest whole number ratio of atoms of each element in the compound

• Calculated from knowledge of the ratio of masses of each element in the compound

Example:
A compound that contains 10 g of Hydrogen and 80 g of Oxygen has an Empirical Formula of H₂O. This can be shown by the following calculations:
Amount of Hydrogen Atoms = Mass in grams ÷ A_r of Hydrogen = (10 ÷ 1) = 10 moles
Amount of Oxygen Atoms = Mass in grams ÷ A_r of Oxygen = (80 ÷ 16) = 5 moles
The Ratio of Moles of Hydrogen Atoms to Moles of Oxygen Atoms:

• Calculate empirical formulae and molecular formulae

Since equal numbers of Moles of Atoms contain the same number of atoms, the Ratio of Hydrogen Atoms to Oxygen Atoms is 2:1
Hence the Empirical Formula is H₂O
Molecular Formula: Gives the exact numbers of atoms of each element present in the formula of the compound

• Divide the relative formula mass of the molecular formula by the relative formula mass of the Empirical Formula
• Multiply the number of each element present in the Empirical Formula by this number to find the Molecular Formula

Relationship between Empirical and Molecular Formula:



Example:
The Empirical Formula of X is C₄H₁₀S₁ and the Relative Formula Mass of X is 180. What is the Molecular Formula of X?
Relative Formula Mass:       Carbon : 12      Hydrogen : 1      Sulfur : 32
Step 1 – Calculate Relative Formula Mass of Empirical Formula
(C x 4) + (H x 10) + (S x 1)    =   (12 x 4) + (1 x 10) + (32 x 1)   =   90
Step 2 – Divide Relative Formula Mass of X by Relative Formula Mass of Empirical Formula
               180 / 90 = 2
Step 3 – Multiply Each Number of Elements by 2
(C_{4 x 2}) + (H_{10 x 2}) + (S_{1 x 2})     =    (C₈) + (H₂₀) + (S₂)
                                 Molecular Formula of X = C₈H₂₀S₂

Calculate percentage yield and percentage purity

Percentage yield

• This is the calculation of the percentage yield obtained from the theoretical yield.
• In practice, you never get 100% yield in a chemical process for several reasons.
• These include some reactants being left behind in the equipment, the reaction may be reversible or product may also be lost during separation stages.

Equation:
Percentage Yield     =    (Yield Obtained / Theoretical Yield) x 100
Example:
In an experiment to displace copper from copper sulfate, 6.5 g of Zinc was added to an excess of copper (II) sulfate solution. The copper was filtered off, washed and dried. The mass of copper obtained was 4.8 g. Calculate the percentage yield of copper.
Equation Of Reaction:    Zn (s)    +    CuSO₄ (aq)     →     ZnSO₄ (aq)    + Cu (s)
Step 1: Calculate the Amount, in Moles of Zinc Reacted
Moles of Zinc = 6.5 ÷ 65 = 0.10 moles
Step 2: Calculate the Maximum Amount of Copper that could be formed from the Molar ratio
Maximum Moles of Copper = 0.10 moles (Molar ratio is 1:1)
Step 3: Calculate the Maximum Mass of Copper that could be formed
Maximum Mass of Copper = ( 0.10 x 64 ) = 6.4 g
Step 4: Calculate the Percentage of Yield of Copper
              Percentage Yield = ( 4.8 ÷ 6.4 ) x 100 = 75%
                                                                 Percentage Yield of Copper = 75%

Percentage purity

• Often the product you are trying to fabricate may become contaminated with unwanted substances such as unreacted reactants, catalysts etc.

Equation:
Percentage Purity = (Mass of pure substance / Mass of impure substance) x 100
Example:
In an experiment 7.0g of impure calcium carbonate were heated to a very high temperature and 2.5g of carbon dioxide were formed. Calculate the percentage purity of the calcium carbonate.
Equation Of Reaction:    CaCO₃ (s)    →     CaO(s)    + CO₂ (g)
Step 1: Calculate the relative formula masses
1 mole CaCO₃ → 1 mole CO₂
40+12+(3×16)      12+(2×16)
100 → 44
Step 2: Calculate the theoretical mass of calcium carbonate used if pure
From 2.5g CO₂ we would expect 2.5/44 x 100 = 5.68g
Step 3: Calculate the percentage purity
(Mass of pure substance / mass of impure substance) x 100
= 5.68/7.0 x 100
= 81.1%

11.4 Carbon dioxide and methane

• State that carbon dioxide and methane are greenhouse gases and explain how they may contribute to climate change

• State the formation of carbon dioxide:

• –  as a product of complete combustion of

• carbon-containing substances

• –  as a product of respiration

• –  as a product of the reaction between an acid and a carbonate

• –  from the thermal decomposition of a carbonate

• State the sources of methane, including decomposition of vegetation and waste gases from digestion in animals

• 
  

• Describe the carbon cycle, in simple terms, to include the processes of combustion, respiration and photosynthesis